The Road to Monads 1: Functors in Haskell

This is the first article in a series on understanding monads in Haskell. Once you have finished this post, feel free to check out the others below:

1. Functors in Haskell
2. Applicative Functors
3. Understanding Monads
4. Parsing Arithmetic with Monads

In Haskell, performing simple input and output operations requires a rudimentary understanding of category theory, a branch of advanced mathematics, which can be incredibly intimidating for newcomers to the language. This series is aimed at making Haskell monads more accessible by building and intuitive and practical understading of monads in Haskell like IO, Maybe and [], one step at a time. We will start by analysing functors, a superclass of monads, and then working our way up to monads in the next few instalments. This series finishes with a hands-on example of using monads to write an elegant ~60 line arithmetic expression parser.

Note to C++ programmers: functors in Haskell are an entirely different concept to C++ functors.

Functors in Haskell

A Haskell functor is a type constructor wrapper for some type of data, paired with a function fmap that lets you apply functions to values stored inside the wrapper. Functors are a very common construct in Haskell, including Maybe, [] and IO among their ranks. We can also define our own functors, for instance a BinaryTree type.

Lists, optionals, and every other functor all contain zero or more values of a specified type of data. You have probably noticed that working with lists and Maybe values can be a little tricky, because you cannot apply ordinary functions to them. For example, (^2) [1,2,3] and Just 1 + Just 2 both do not typecheck. This is because neither [Int] nor Maybe Int belong to the Integral typeclass which (^2) works for, only Int itself does. In order to work with these types, we have to apply a function to the values inside the functor. To do this, we can pattern match over their constructors to unwrap their values:

squareList :: Num a => [a] -> [a]
squareList [] = []
squareList (x:xs) = x^2 : squareList xs
-- OR: squareList xs = [ x^2 | x <- xs ]

addMaybes :: Num a => Maybe a -> Maybe a -> Maybe a
addMaybes (Just a) (Just b) = Just (a + b)
addMaybes _ _ = Nothing

This is rather tedious, especially in the case of lists. What do good programmers do when they see repetitive code? They create abstractions. In the first case, we can create a function to generalise this pattern-matching process to work for any function, not just (^2). Below is a function fmapList which does exactly that. For the second case, binary functions are a little trickier. In fact, functors alone cannot be used to abstract away pattern matching for binary functions; instead Applicative Functors, covered in the next article, must be used.

fmapList :: (a -> b) -> ([a] -> [b])
fmapList f [] = []
fmapList f (x:xs) = f x : fmapList f xs

squareList = fmapList (^2)

An astute reader may notice this is the same as the function map, which lets you provide a function and a list, and applies the function to every value in the list. We can also partially apply just a function of type a -> b. This ‘promotes’ our function to work on lists, as the returned function has the type [a] -> [b].

What functors do is take this abstraction one step further. Every functor has a function fmap, of which map for lists is a special case. fmap takes a normal function a -> b, and promotes it to work for some functor f by returning a function of type f a -> f b. f could be [] or Maybe or any other type constructor with a Functor instance. For instance, fmap (^2) in the context of lists generates a function that maps the square function over a list. For Maybe values, fmap (^2) will square a Just value, but leave a Nothing value alone. If we defined a BinaryTree type, we could define fmap to apply a function to every value in a tree.

Technically, a functor is a type constructor that is defined as an instance of the Functor typeclass, paired with a function fmap. Functors are a superset of monads, so to define a Monad instance you must first define a Functor instance. It is important to stress that both the type constructor and the fmap function are technically the functor from a math standpoint, as neither in isolation forms a functor. You can think of the type constructor of a functor as a function which converts one representation of an object (eg Int) to another with the same underlying structure, but different form (eg Maybe Int). Then the fmap function converts one representation of a function to another which can be used on our mapped types. Each functor has a different implementation of fmap depending on how it is used, so fmap f is a polymorphic function which can work on any functor depending on context.

Functors have to adhere to several laws which the compiler cannot check for you. This means it is possible to write invalid Functor instances, which may result in strange behaviour when using standard library functions which assume the functor laws hold. The functor laws are as follows.

1. Identity: fmap id == id.
2. Composition: fmap (f . g) == fmap f . fmap g.

As a challenge, you could try proving these hold for the three functor instances we derive in the rest of the article.

Deriving the [] and Maybe Functors

Now we will demonstrate how to define some common Functor instances to show how they work. We will start with [], as we already know that map is actually a special case of fmap. In fact, the following snippet is the exact definition of Functor [] in the Prelude standard library!

instance Functor [] where
  fmap = map

You can substitute map for fmap anywhere in your code, and they will accomplish the same purpose: applying a function to all values stored inside a list.

We will now derive the Functor Maybe instance. If we want to square a Maybe value, we can write the following code using pattern matching:

squareMaybe :: Maybe Int -> Maybe Int
squareMaybe (Just x) = Just (x^2)
squareMaybe Nothing = Nothing

The pattern matching approach works, but it is a lot of work, and you have to pattern match on every function you want to use. This increases clutter, decreases portability, and increases the likelihood of bugs. Once again we will abstract away the pattern matching, defining a function fmap'. This applies a function you provide to each value inside a functor, which in this case is Maybe. It will take a function, and a Maybe Int value, and return a new Maybe Int.

fmap' :: (Int -> Int) -> (Maybe Int -> Maybe Int)
fmap' f (Just x) = Just (f x)
fmap' f Nothing = Nothing

squareMaybe :: Maybe Int -> Maybe Int
squareMaybe = fmap' (^2)

main = print (squareMaybe (Just 3))
-- prints 3^2==9

This means we can easily apply any function inside our Maybe functor. However, what if we want to take the square root? Then we need to apply a function Int -> Double, which our fmap' does not support. To do this, we take it to a higher level of abstraction, with polymorphic input and output types using type variables:

fmap' :: (a -> b) -> Maybe a -> Maybe b
fmap' f (Just x) = Just (f x)
fmap' f Nothing = Nothing

sqrtMaybe :: Maybe Int -> Maybe Double
sqrtMaybe = fmap' (sqrt . fromIntegral)
-- equiv. to: fmap' (\x -> sqrt (fromIntegral x))

main = print (sqrtMaybe (Just 3))
-- prints 1.73...

We can now define a simple Functor Maybe instance. If you check the standard library you will once again see the implementations are equivalent.

instance Functor Maybe where
  fmap f (Just x) = Just (f x)
  fmap _ Nothing = Nothing

We can now write fmap (^2) (Just 2) to get Just 4, for instance.

The IO Functor

Another crucial example of a functor, which behaves a little differently to the rest, is the IO type constructor. In Haskell, everything is a pure function as you may know. However, if you have no input or output, which are impure actions, all programs do is produce heat. In order to elegantly allow IO operations, the type constructor IO denotes a value which is used for input or output. This means any impure functions must have IO in their type signature, so it is impossible for a pure, non-IO function to exhibit side effects unless it uses the unsafePerformIO escape hatch.

When you run an IO operation such as getLine, the return value is wrapped in the IO functor as an IO String. In order to apply a pure function to its value, we need to use fmap:

import Data.Char (toUpper)
stringToUpper :: String -> String
-- remember String is a type alias for [Char]
-- toUpper works on Char, so we map or fmap it
stringToUpper = fmap toUpper

main = do
  -- apply stringToUpper to the value inside getLine
  a <- fmap stringToUpper getLine
  putStrLn a

If you are familiar with do syntax, you may recognise that you can equivalently write main = do { a <- getLine; putStrLn (stringToUpper a) }, removing the need for fmap. However, this syntactic sugar is converted to main = getLine >>= putStrLn (stringToUpper a), which uses the >>= (‘bind’) function for monads. Monads are a subclass of functors, and so the definition of >>= actually depends on fmap internally. Thus, to do anything meaningful with IO in Haskell, you are implicitly using fmap.

Creating a BinaryTree Functor

If we define a data type BinaryTree a, a binary tree storing type a, we can show it is a functor and use fmap to apply a function to every value in the tree, similar to map on lists. We define a binary tree recursively using algebraic data types.

data BinaryTree a = Node a (BinaryTree a) (BinaryTree a) | Leaf a

{- Usage: the below tree is: Node 1 (Node 2 (Leaf 3) (Leaf 5)) (Leaf 6)
    1
   / \
  2   6
 / \
3   5   -}

Then, the functor instance for BinaryTree is as follows. This fmap definition recursively computes a new tree where each value has had the function applied to it. This means we can write very terse code to perform operations over entire data structures.

instance Functor BinaryTree where
  fmap f (Node x left right) = Node (f x) (fmap f left) (fmap f right)
  fmap f (Leaf x) = Leaf (f x)

Ultimately, the advantage of creating the Functor abstraction then is that we can write very code at a much higher level of abstraction which reduces boilerplate and lets us write very concise, elegant Haskell code. It also allows us to write code that is polymorphic with respect to all functors. We can write functions that work for any functor like below:

squareAllInFunctor :: (Functor f, Num a) => f a -> f a
squareAllInFunctor = fmap (^2)
squareAllInFunctor [1,2,3] == [1,4,9]
squareAllInFunctor (Just 3) == Just 9
-- two layers of functors (need to fmap twice, ie 'fmap (fmap (^2))')
fmap squareAllInFunctor [Just 2, Nothing, Just 5 ]
                     == [Just 4, Nothing, Just 25]
-- our binary tree
squareAllInFunctor Node 1 (Node 2 (Leaf 3) (Leaf 5 )) (Leaf 6 )
                == Node 1 (Node 4 (Leaf 9) (Leaf 25)) (Leaf 36)

Mathematical Background

In order to effectively use functors, monads, categories and other ideas from category theory in Haskell, an in-depth understanding of category theory is not required. However, having a rudimentary understanding of them cannot hurt, and will make it easier to understand their counterparts in Haskell. You can comfortably skip this section if you find it too dense or just want to understand how to use Haskell functors in practice.

A category is a set of objects and arrows. Graphically categories resemble directed graphs. Arrows between objects (also called morphisms) are effectively functions that map one object to another. Categories are at a very high level of abstraction where depending on context the objects and arrows could represent anything. We will deal with only two categories: Set, and Hask.

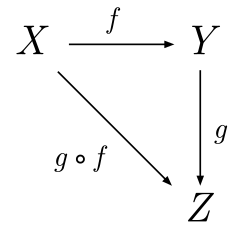Diagram of a simple category with objects A,B,C and arrows f, g, g∘f (arrow composition).

Set is the category of sets. Every object in Set is a mathematical set. Every arrow in Set is a function from one set to another. For instance, the function/mapping/morphism/arrow \(f(x) = \sin x\) is a rule describing one possible arrow from the domain set \(\mathbb{R}\) to the range set \([-1, 1]\).

Hask is similar to Set, however the objects are Haskell types like Int or Double instead of \(\mathbb{Z}\) or \(\mathbb{R}\). The arrows between two objects a and b are Haskell functions of type a -> b. Note that a -> b is also a type, and so is also an object in Hask. The only other noteworthy difference is that some functions are impossible to evaluate in Haskell because they run into infinite loops, however this can be safely ignored (for more information see here). For simplicity, we will say that Set and Hask are isomorphic, meaning they have equivalent structure. That is, for every mapping or set in Set, there is a corresponding function or type in Hask.

An important idea in category theory is that of composition. If there is an arrow from A to B, and B to C, we can compose the two arrows to create one from A to C. This is equivalent to function composition in Hask. It is also important to note that every object has an arrow to itself, called the identity id, which is like id x = x, which when composed, acts as an identity: id . f = f . id = f. This works because function composition forms a monoid.

A functor is a map between categories, say C and D. This means it can map any object or arrow from C to an isomorphic object or arrow in D. Now we can get really meta: in the category of categories, the arrows are called functors, as they map one category to another.

In Haskell, we can only work within Hask, so functors all map back to Hask. Thus all functors represented by Haskell’s Functor typeclass are a special type of functor called endofunctors, which map a category back to itself. Note that even though they map back to the same place like id does, they are not identities.

Remember that a functor can map any object or arrow. This means Haskell functors consist of a function from one type to another, and a function from one function to another. This may seem very complex at face value, but bear with me. A type constructor like TypeCtor in newtype TypeCtor a = ValueCtor a can be thought of as function from one type to another. For example, TypeCtor applied to Int produces a new type called TypeCtor Int. Type constructors are the only way to create type level functions in Haskell, so by definition functors in Haskell must lift a type a to a type TypeCtor a.

Secondly, we need a function we’ll call fmap (short for “functor map”) that maps one function to another. If we were working with two categories C and D, fmap would take an arrow between two objects in C and map it to the corresponding arrow between two corresponding objects in D. We are working only in Hask, so we will map a function between normal types a -> b to the corresponding types created by the type constructor in our functor. That is, we map any function a -> b to the corresponding function TypeCtor a -> TypeCtor b.

This means a functor in Haskell is a type constructor f a paired with a function fmap :: (a -> b) -> (f a -> f b) which ‘promotes’ normal functions to work within our functor. The two components are summarised below:

1. f :: * -> *: A type constructor which takes one type a and produces another isomorphic type f a. This maps one object in Hask to another isomorphic object.
2. fmap :: (a -> b) -> (f a -> f b): A function which takes any normal function and ‘promotes’ it to work with values of the new types we defined (eg f a). This maps one arrow in Hask to another isomorphic arrow.

Note that the type variable f refers to the type constructor of some functor, and a and b refer to any concrete types (meaning they are not type constructors).

If you want to learn more about category theory from the perspective of a programmer, I cannot recommend Bartosz Milewski’s Category Theory for Programmers enough.

In the next article, we introduce applicative functors, or applicatives, which are functors which allow us to use functions of multiple arguments very concisely. Then, in part three we will introduce monads, which are a subclass of both functors and applicatives.

Part 2: Applicative Functors

Source Code: Functors.hs